PERIODIC TEST I (2022-23)
SUBJECT : PHYSICS
CLASS : XII
MM.:30
Time : 1 Hour
Intructions:
(i) All questions are compulsory. There are 12 questions in all.
(ii) Question no. 1-2 are of one mark each, Question no. 3-6 are of two marks each, Question no. 7-11 are of three marks each & Question no. 12 is of five marks.
Q1. Why must electrostatic field be normal to the surface at every point of a charged conductor?
Q.2 In which orientation, a dipole placed in a uniform field is in (a) stable and (b) unstable equilibrium?
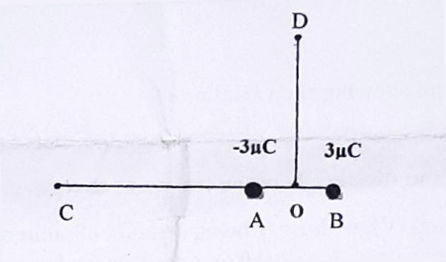
Q.3 Two point charges +3µC and -3µC are located at points A and B, 2 mm apart in vacuum, determine the direction of the force experienced by the test charge q₀ at points C, O and D. (O at centre of AB, OC=OD=1m). Compare the force on the test charge at points C and D.
Q.4 In a type of charge configuration electric field at a point due to it is i) independent of distance from the point ii) inversely proportional to the distance from the point iii) inversely proportional to the square of diatnce from the point iv) inversely proportional to the cube of distance from the point indentify the type of charge configuration in each case.
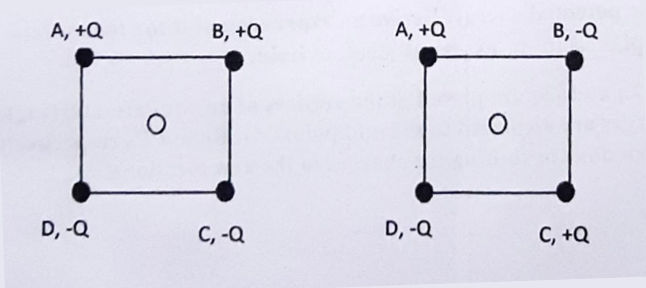
Q.5 Four point charges are placed at the four corners of a square in the two ways as shown in figure (a) and (b). Will the 1) Electric field and 2) Electric Potential at the centre of the square be same or different in the two configurations and why?
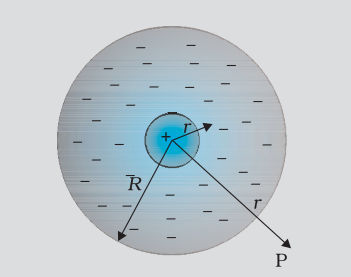
Q.6 An early model for an atom considered it to have a positively charged nucleus of charge Ze, surrounded by a uniform density of negative charge up to a radius R. The atom as a whole is neutral. For this model, what is the electric field at a distance ‘r’ from the nucleus when r<R?
Q.7 Deduce an expression for electric field due to an electric dipole on its equatorial line.
Q.8 Three small identical conducting spheres A, B & C have charges -3×10-12C, 8×10^-12C and 4×10^-12C respectively. They are brought in contact and then placed at vertices of equilateral triangle as shown in fig. Calculate (i) charge on each sphere after separation (ii) number of electrons in excess or deficit on sphere after separation. (iii) direction of net force at charge at C.
Q.9 Plot the graph showing the variation of
(i) electric field and potential with distance from the centre of a point charge (on same graph).
(ii) electric force and distance between two point charges q1 and q2 for q1q2<0, and (iii) electric potential (V), with 1/r (r being distance of point of observation from the centre of point charge) for two charges q1 and q2, q1>0 and q2<0, as well as |q1|<|q2|.
Q.10 (a) Draw electric field lines due to two unequal like point charges.
(b) describe schematically equi potential surfaces for the following cases i) uniform electric field along z-direction ii) an electric field that uniformly increases in magnitude but remains same in x-direction.
Q.11 The electric field at a distance of 20 cm and 40 cm from a specific charge configuration is same. Identify such system of charges and deduce an expression for electric field at any point due to it.
Q.12 (a) Define electrostatic potential energy. Drive an expression of it for the system of two point charges when placed in an external electric field.
(b) Three point charges q, 2q and -3q are placed at the vertices of an equlateral triangle ABC of side L. If these charges are displaced to the mid points A1, B1 and C1 respectively, calculate the amount of work done in shifting the charges to the new locations.

OR
(a) State Gauss theorem and use it to determine electric field due to infinitely long uniformly charges wire of linear charge density λ.
(b) If a dipole of dipole moment 2aq placed in the neighbourhood of this charged wire such that its axis is parallel to line charge wire, then deduce the net force and net torque on the dipole.